Contact

OpenCV: Keypoint Descriptors

Robert Taylor • April 23, 2019
MathematicsOpenCVPython

This is a very quick post showing how to instantiate and compute descriptors in OpenCV. I include 4 binary descriptors (FREAK, BRIEF, BRISK, and ORB) and two non-binary descriptors (SIFT and SURF).

Environment:

  • Python 3.6
  • OpenCV 4.1
import numpy as np
import matplotlib.pyplot as plt
import cv2

I took two pictures of my cat Charlie at slightly different angles. Then I selected by hand a pair of matching keypoints. Of course, I could have employed a detector for this task (FAST, AGAST, ORB, etc.), but I wanted to keep this post short and focused solely on descriptors. The two JPG images:

# first cat image
C1 = cv2.imread('cat1.jpg')
C1_gr = cv2.cvtColor(C1, cv2.COLOR_BGR2GRAY)


# second cat image
C2 = cv2.imread('cat2.jpg')
C2_gr = cv2.cvtColor(C2, cv2.COLOR_BGR2GRAY)


# hand-pick a keypoint
kp1 = (719, 769)
kp2 = (903, 728)


# show images
marker_style = {
    'markersize': 15,
    'markeredgewidth': 3,
    'markeredgecolor': 'w',
    'markerfacecolor': 'None',
    }
f, ax = plt.subplots(1, 2, figsize=(14, 7))
ax[0].imshow(C1_gr, cmap='hot', interpolation='none')
ax[0].plot(*kp1, 'o', **marker_style)
ax[0].set_title('cat 1')
ax[1].imshow(C2_gr, cmap='hot', interpolation='none')
ax[1].plot(*kp2, 'o', **marker_style)
ax[1].set_title('cat 2')
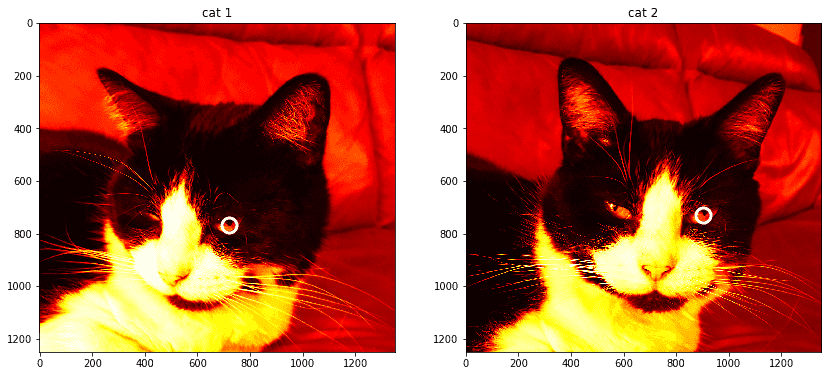
output

Then, for comparison, I generated a small assortment of random points for each image and paired them.

def rand_coords(n, img_shape):
    # usage: rand_coords(20, C1_gr.shape)
    return (np.random.rand(n, 2) @ np.diag(img_shape)).astype(int)


# 8 random points in "cat1.jpg"
rnd_pts_1 = np.array(
    [[ 266, 1147],
     [ 896,  884],
     [ 385,  566],
     [ 468,  141],
     [ 889, 1084],
     [ 549, 1029],
     [ 987,  145],
     [ 419,  931]])


# 8 random points in "cat2.jpg"
rnd_pts_2 = np.array(
    [[ 811,  980],
     [1176,  716],
     [ 259,  340],
     [ 745,  952],
     [ 265,  730],
     [ 852,  774],
     [1019, 1127],
     [ 660, 1110]])


# show images
f, ax = plt.subplots(1, 2, figsize=(14, 7))
ax[0].imshow(C1_gr, cmap='gray', interpolation='none')
ax[0].set_title('cat 1')
ax[1].imshow(C2_gr, cmap='gray', interpolation='none')
ax[1].set_title('cat 2')
for i in range(rnd_pts_1.shape[0]):
    label = 'rand-' + str(i+1)
    _marker_style = dict(marker_style)
    _marker_style['markeredgecolor'] = 'C' + str(i if i < 7 else i+1)
    ax[0].plot(*rnd_pts_1[i], 'o', label=label, **_marker_style)
    ax[1].plot(*rnd_pts_2[i], 'o', label=label, **_marker_style)
ax[1].legend(
    loc='upper left',
    bbox_to_anchor=(1.05, 1),
    borderaxespad=0.0,
    labelspacing=1,
    borderpad=1)
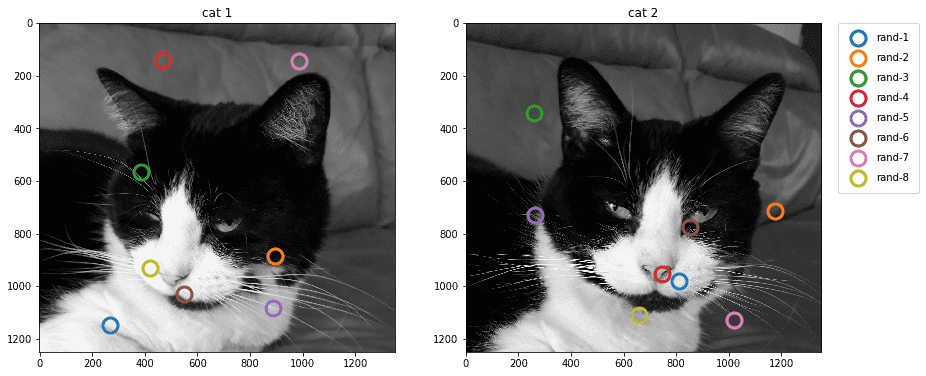
output

Everything is all prepared to compute descriptors and measure their distance from one another.

FREAK: Fast Retina Keypoint

Code:

def get_bin_desc(extractor, img, kp, size=30):
    # extract a binary descriptor from the image
    d = extractor.compute(img, [cv2.KeyPoint(*kp, size)])[1][0]
    return np.unpackbits(d)


def get_hamming_dist(d1, d2):
    # return the Hamming distance
    return np.sum(np.logical_xor(d1, d2))


def run_bin_test(extractor):
    # print Hamming distances between keypoints using the binary extractor


    d1 = get_bin_desc(extractor, C1_gr, kp1)
    d2 = get_bin_desc(extractor, C2_gr, kp2)
    dist = get_hamming_dist(d1, d2)


    print('Hamming distance of pairs (out of {})\n'.format(len(d1)))
    print('Hand-picked: {:3d}'.format(dist))


    for i in range(rnd_pts_1.shape[0]):
        d1 = get_bin_desc(extractor, C1_gr, rnd_pts_1[i])
        d2 = get_bin_desc(extractor, C2_gr, rnd_pts_2[i])
        dist = get_hamming_dist(d1, d2)


        print('Random {}:    {:3d}'.format(i+1, dist))


extractor = cv2.xfeatures2d_FREAK.create()
run_bin_test(extractor)

Output:

Hamming distance of pairs (out of 512)


Hand-picked:  67
Random 1:    220
Random 2:    170
Random 3:    207
Random 4:    367
Random 5:    165
Random 6:    292
Random 7:    272
Random 8:    257

BRIEF: Binary Robust Independent Elementary Features

Code:

extractor = cv2.xfeatures2d_BriefDescriptorExtractor.create()
run_bin_test(extractor)

Output:

Hamming distance of pairs (out of 256)


Hand-picked:  37
Random 1:    139
Random 2:    161
Random 3:     55
Random 4:     95
Random 5:    134
Random 6:    158
Random 7:     86
Random 8:    123

BRISK: Binary Robust Invariant Scalable Keypoints

Code:

extractor = cv2.BRISK.create()
run_bin_test(extractor)

Output:

Hamming distance of pairs (out of 512)


Hand-picked: 101
Random 1:    296
Random 2:    180
Random 3:    171
Random 4:    289
Random 5:    210
Random 6:    311
Random 7:    192
Random 8:    241

ORB: Oriented FAST and Rotated BRIEF

Code:

extractor = cv2.ORB.create()
run_bin_test(extractor)

Output:

Hamming distance of pairs (out of 256)


Hand-picked:  35
Random 1:    167
Random 2:    170
Random 3:     92
Random 4:    130
Random 5:    102
Random 6:    183
Random 7:     91
Random 8:    136

SIFT: Scale Invariant Feature Transform

Code:

def get_non_bin_desc(extractor, img, kp, size=30):
    # extract a non-binary descriptor from the image
    return extractor.compute(img, [cv2.KeyPoint(*kp, size)])[1][0]


def get_l2_dist(d1, d2):
    # return the L2 distance
    return np.linalg.norm(d2-d1)


def run_l2_test(extractor):
    # print L2 distances between keypoints using the non-binary extractor


    d1 = get_non_bin_desc(extractor, C1_gr, kp1)
    d2 = get_non_bin_desc(extractor, C2_gr, kp2)
    dist = get_l2_dist(d1, d2)


    print('L2 distance of pairs\n')
    print('Hand-picked: {:.3f}'.format(dist))


    for i in range(rnd_pts_1.shape[0]):
        d1 = get_non_bin_desc(extractor, C1_gr, rnd_pts_1[i])
        d2 = get_non_bin_desc(extractor, C2_gr, rnd_pts_2[i])
        dist = get_l2_dist(d1, d2)


        print('Random {}:    {:.3f}'.format(i+1, dist))


extractor = cv2.xfeatures2d_SIFT.create()
run_l2_test(extractor)

Output:

L2 distance of pairs


Hand-picked: 231.288
Random 1:    413.424
Random 2:    557.979
Random 3:    425.087
Random 4:    427.973
Random 5:    520.956
Random 6:    367.421
Random 7:    523.169
Random 8:    548.730

SURF: Speeded Up Robust Features

Code:

extractor = cv2.xfeatures2d_SURF.create()
run_l2_test(extractor)

Output:

L2 distance of pairs


Hand-picked: 0.483
Random 1:    0.741
Random 2:    0.784
Random 3:    0.940
Random 4:    1.009
Random 5:    1.009
Random 6:    1.074
Random 7:    0.778
Random 8:    0.753

References

  1. Alahi, Alexandre, Raphael Ortiz, and Pierre Vandergheynst. “Freak: Fast retina keypoint.” 2012 IEEE Conference on Computer Vision and Pattern Recognition. Ieee, 2012.
  2. Calonder, Michael, et al. “Brief: Binary robust independent elementary features.” European conference on computer vision. Springer, Berlin, Heidelberg, 2010.
  3. Leutenegger, Stefan, Margarita Chli, and Roland Siegwart. “BRISK: Binary robust invariant scalable keypoints.” 2011 IEEE international conference on computer vision (ICCV). Ieee, 2011.
  4. Rublee, Ethan, et al. “ORB: An efficient alternative to SIFT or SURF.” ICCV. Vol. 11. No. 1. 2011.
  5. D. Lowe. “Distinctive Image Features from Scale-Invariant Keypoints.” Accepted for publication in the International Journal of Computer Vision. 2004.
  6. Bay, Herbert, Tinne Tuytelaars, and Luc Van Gool. “Surf: Speeded up robust features.” European conference on computer vision. Springer, Berlin, Heidelberg, 2006.

GET IN TOUCH

Have a project in mind?

Reach out directly to hello@humaticlabs.com or use the contact form.

Contact Us

HUMATIC LABS LLC

All rights reserved